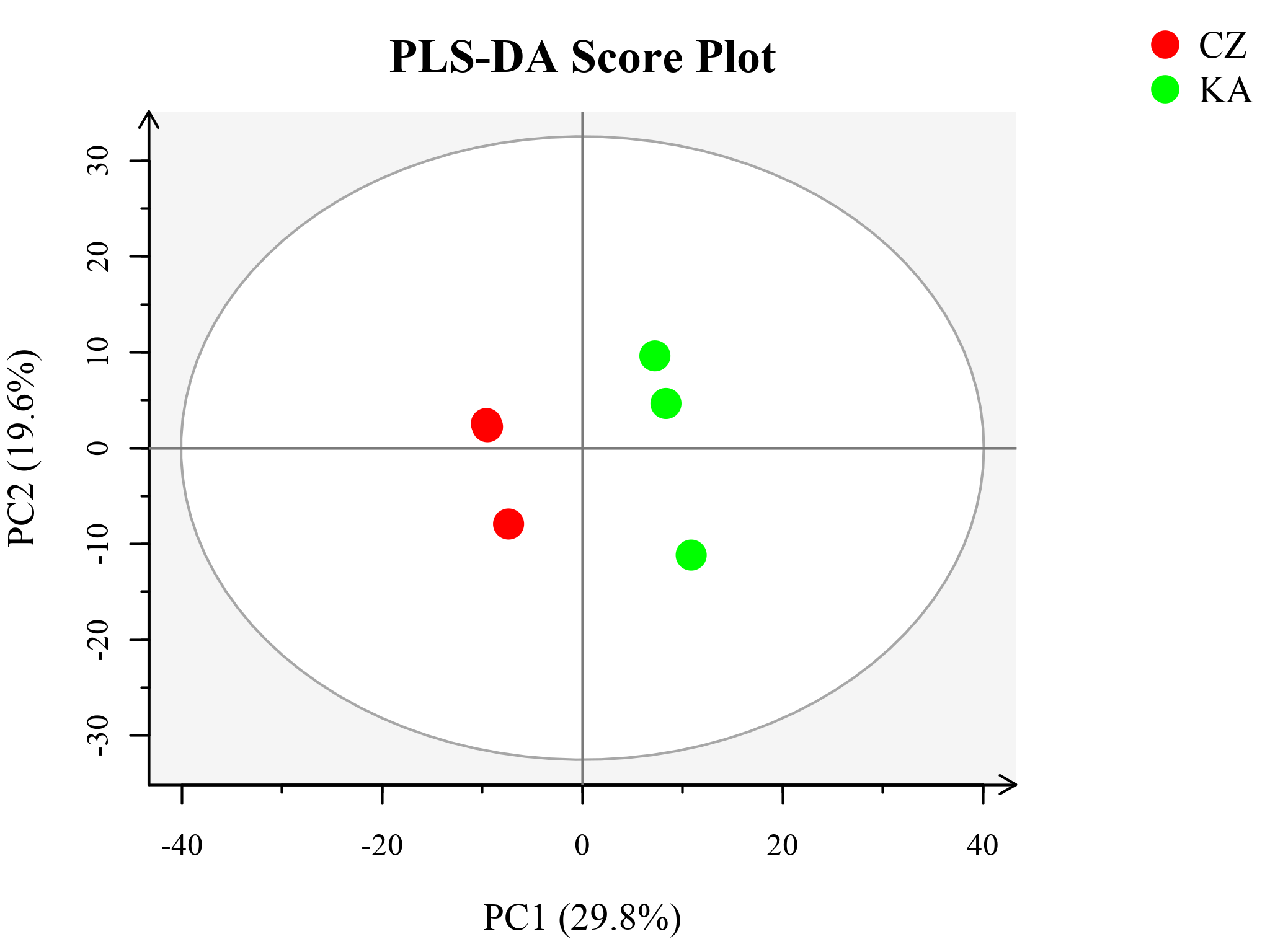
偏最小二乘法-判别分析(PLS-DA)
无监督分析方法(unsupervised analysis,如PCA)不能忽略组内误差、消除与研究目的无关的随机误差,过分关注于细节、忽略了整体和规律,最终不利于发现组间差异和差异化合物。在这种情况下,就需要利用样本的先验知识将数据分析进一步聚焦到我们要研究的方面,采用有监督模式识别方法(supervised analysis),如偏最小二乘法-判别分析(partial least squares-discriiminate analysis, PLS-DA)。
与PCA只有一个数据集不同,PLS-DA在分析时必须对样品进行指定并分组,这样模型会自动加上另外一个隐含的数据集Y,该数据集变量数等于组别数。PLS-DA是目前代谢组学数据分析中最常使用的一种分类方法,它在降维的同时结合了回归模型,并利用一定的判别阈值对回归结果进行判别分析。
PLS与PCA不同之处在于PLS即分解自变量X矩阵,也分解因变量Y矩阵,并在分解时利用其协方差信息,从而使降维效果较PCA能够更高效的提取组间变异信息[1]。
模型的交叉验证主要参考R2X、R2Y、Q2 等参数[2] ,R2X是模型X变量(自变量)的可解释度,R2Y为模型Y变量(因变量)的可解释率,Q2是模型的可预测度(通常情况下,R2、Q2高于0.5较好,且两者差值不应过大,R2和Q2最大值为1)。当R2值较小时,往往意味着测试集中重复性较差(背景噪音高时);Q2值较小时,表示测试集中具有较高的背景噪音,或者模型具有较多的异常样本(outlier)。
因为PLS-DA在建模时对样品进行了指定和分组,所以能更大地区分组间差异,但这也导致数据的PLS-DA模型存在过拟合(overfitting)的问题。
置换检验图(Permutations Plot)能帮助有效评估当前PLS-DA模型是否过拟合。评判标准为(满足其中任意一个即可)[3]:[1]. 所有蓝色的Q2点从左到均低于最右的原始的蓝色的Q2点;[2]. Q2点的回归线在纵坐标的交叉点小于等于0。