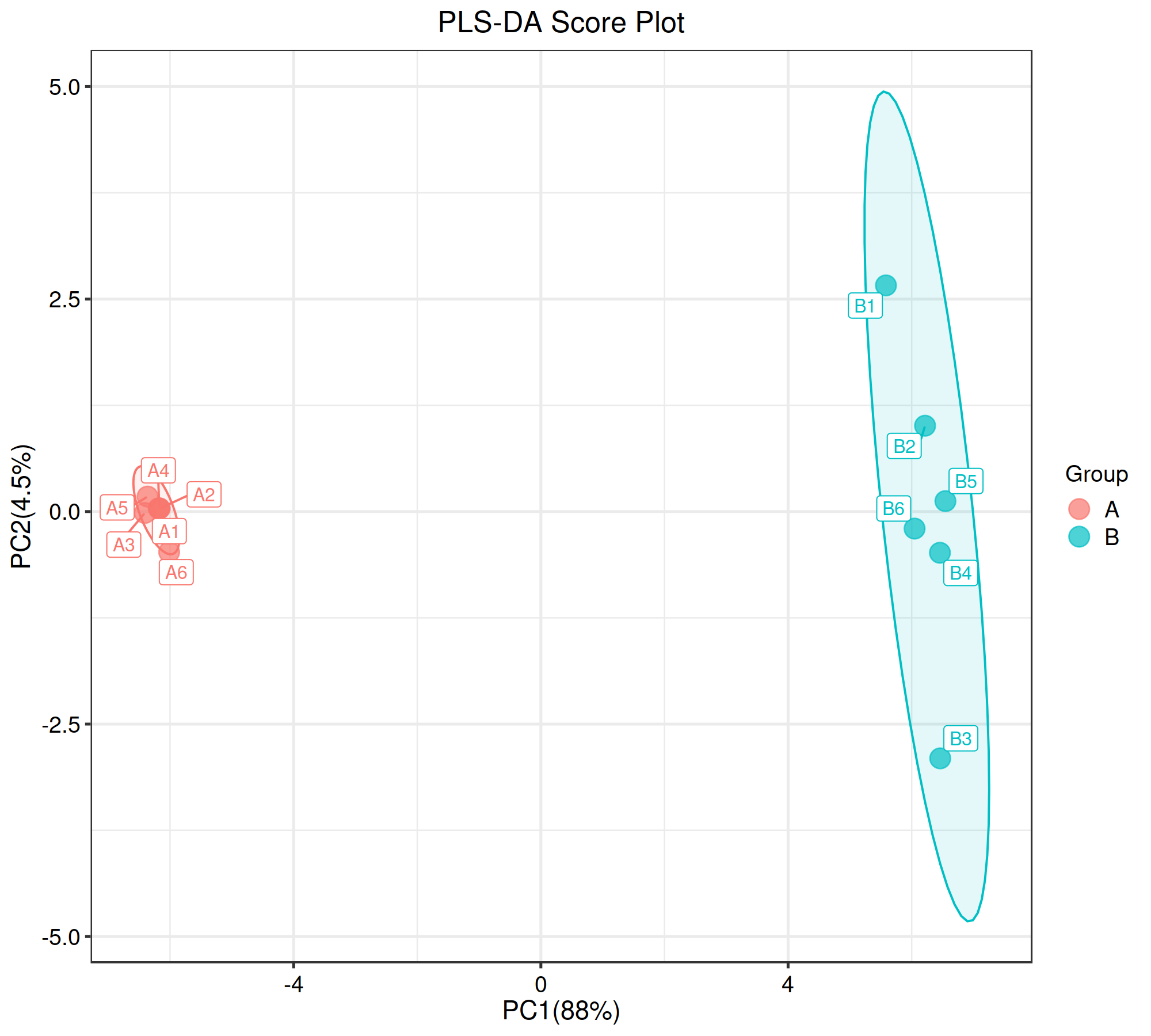
偏最小二乘法判别分析（Partial Least Squares Discrimination Analysis, PLS-DA）是一种有监督的判别分析统计方法。该方法运用偏最小二乘回归建立代谢物表达量与样品类别之间的回归模型，来实现对样品类别的预测。建立各比较组的PLS-DA模型，经交叉验证得到模型评价参数R2（模型可解释度）和Q2（模型可预测度），如果R2和Q2越接近 1，表明模型越稳定可靠。

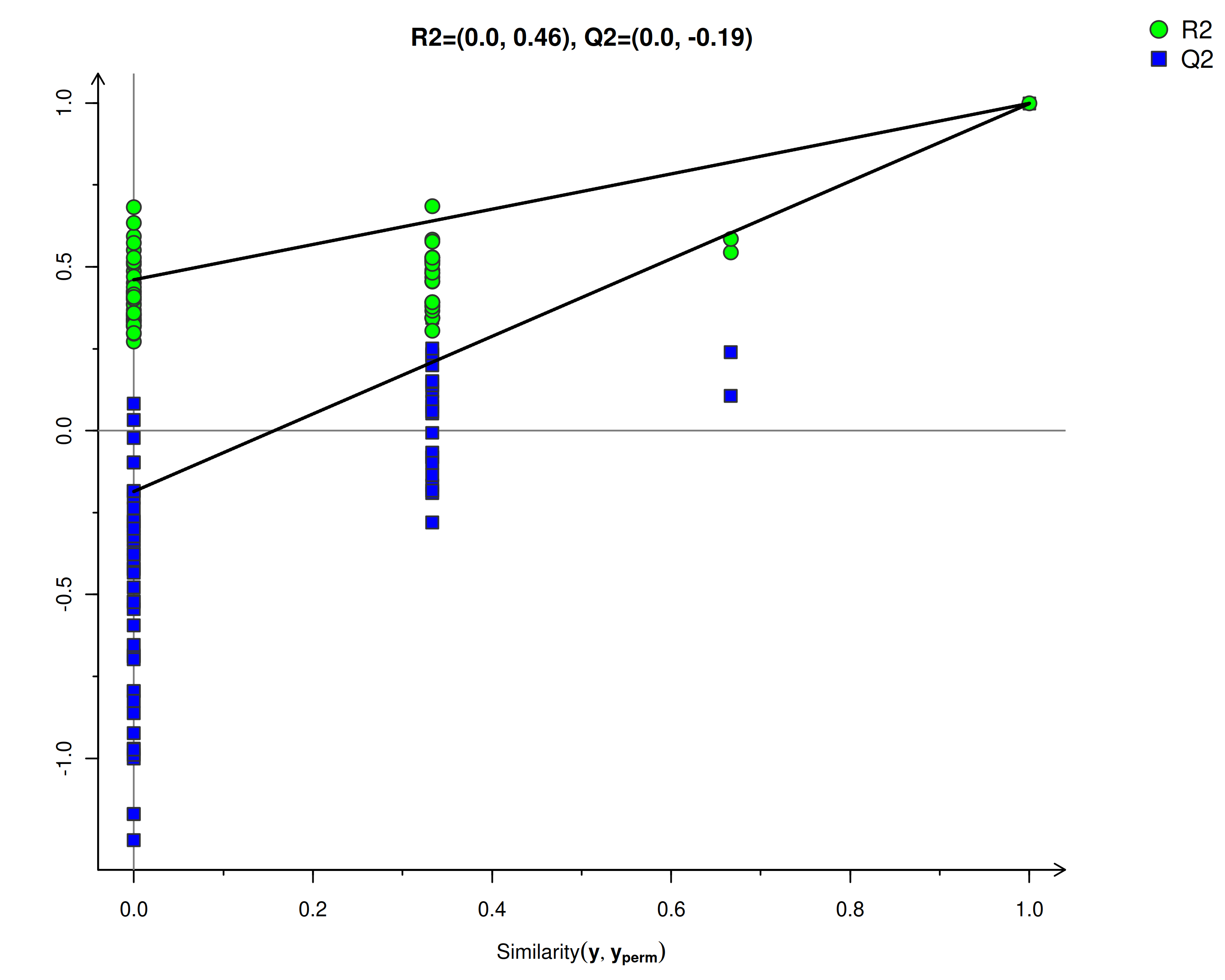
为了判别模型质量好坏，还会对模型进行排序验证即置换检验，检验模型是否“过拟合”。模型是否过拟合体现了模型构建是否准确，未过拟合说明模型能较好的描述样本，并可作为模型生物标记物群寻找的前提，“过拟合”则说明该模型不适合用来描述样本，也不宜以此数据做后期分析。具体方法是将每个样本的分组标记随机打乱后再进行建模和预测，每次建模都对应着一组R2和Q2的值，，通常来说，预测的R2和Q2小于真实分组的R2和Q2，可以表明模型未“过拟合”。

PLS与PCA不同之处在于PLS即分解自变量X矩阵，也分解因变量Y矩阵，并在分解时利用其协方差信息，从而使降维效果较PCA能够更高效的提取组间变异信息^[1]。

模型的交叉验证主要参考R2X、R2Y、Q2 等参数^[2] ，R2X是模型X变量（自变量）的可解释度，R2Y为模型Y变量（因变量）的可解释率，Q2是模型的可预测度（通常情况下，R2、Q2高于0.5较好，且两者差值不应过大，R2和Q2最大值为1）。当R2值较小时，往往意味着测试集中重复性较差（背景噪音高时）；Q2值较小时，表示测试集中具有较高的背景噪音，或者模型具有较多的异常样本（outlier）。

因为PLS-DA在建模时对样品进行了指定和分组，所以能更大地区分组间差异，但这也导致数据的PLS-DA模型存在过拟合（overfitting）的问题。

置换检验图（Permutations Plot）能帮助有效评估当前PLS-DA模型是否过拟合。评判标准为（满足其中任意一个即可）^[3]：[1]. 所有蓝色的Q2点从左到均低于最右的原始的蓝色的Q2点；[2]. Q2点的回归线在纵坐标的交叉点小于等于0。